概要
データ活用の実務において、前処理は地味で泥臭いながら最も重要な工程の一つです。
前処理とは、活用したい生のデータにおける様々な汚れ、たとえば
- 型の不一致
- 年齢のカラムに数値型の「24」や文字列型の「33歳」が混在するなど
- 異常値の存在
- 金額のカラムの単位で「万円」を指定したのに一部のデータ入力者が「円」だと誤認したために他のデータと桁が違うものが混入したり、年収の分布において平均値に大きく影響を与えてしまう数億円以上の高所得者など
- 欠損値の存在
- データ入力者の作業ミスや、アンケートデータにおいて一部の回答者が回答せず空欄になってしまっている質問など
などを綺麗にして、機械学習モデルや統計モデルで投入可能な形に整形することを指します。
したがって前処理と一口にいっても膨大な話題があり、前処理だけで一冊の本が出来てしまうくらいですが、今回は特に欠損値処理をピックアップし、特にPythonのscikit-learnライブラリに格納されているIterativeImputerを利用した便利な欠損値補完法を紹介します。
理論
IterativeImputerのベースとなる多変量補完とは、その名の通り、欠損が存在する値(ex. 体重)の列をそれ以外の複数の列(ex. 身長、性別、年齢)も活用して予測した値により補完する手法です。
対になる概念は単変量補完ですが、これは上記例でいえば、欠損している体重の値を欠損していない他の体重のデータのみを利用して予測することに相当します。具体的には、平均値や中央値、最頻値などによって補完します。
単変量補完と多変量補完は一見して多変量補完の方が万能なように感じてしまいますが、もちろん良し悪しがあり、場合によっては単変量補完の方が適しているケースもあります。たとえば、以下のようなケースでは多変量補完の恩恵が薄いか、単変量補完の方が有利です。
- 互いに関係性がほとんどない列で構成されているデータ
- 先進国における性別と国籍。新興国では男女比に偏りのある国もあるようですが、先進国では基本的に男女比は1:1と考えられるので、性別からその人の国籍を予測することも、逆に国籍からその人の性別を予測することも困難です。したがって、わざわざ多変量補完を使わなくても、単変量補完で十分だと考えられます。
- 膨大なサイズのデータ
- たとえば100万行×500列のビッグデータを対象とする場合、単変量補完であれば各列に対して100万個の値から平均値などの代表値を500回計算するイメージですが、多変量補完だと5億個の値を一度に活用するため、単変量補完と比べて膨大なメモリ、すなわちPCスペックを必要とします。
- 特に多変量補完においてベイジアンリッジやランダムフォレストなどの機械学習モデルを使おうとすると更にマシンパワーを食うため、無料版のGoogleColabや低スペックなPCではそもそもIterativeImputerが最後まで回らず固まってしまう現象が発生します。このようなケースでは単変量補完を使わざるを得ません。
とはいえ、実務で利用するデータは各列間に何かしらの関係性があるケースの方が多いですし、ビッグデータであってもIterativeImputerで一旦回してみてPCが固まらないようならそのまま使えばいいので、多くの場合において「とりあえずIterativeImputerを使ってみる」戦略が有効な印象です。
実験用データ
今回は、以下の手順により、乱数を用いた1,000行×5列の仮想データを生成します。まず、最初の2列を正規乱数により生成します。
import numpy as np
import pandas as pd
np.random.seed(0)
X = pd.DataFrame(np.random.normal(size=(1000, 2)), columns=['A', 'B'])
X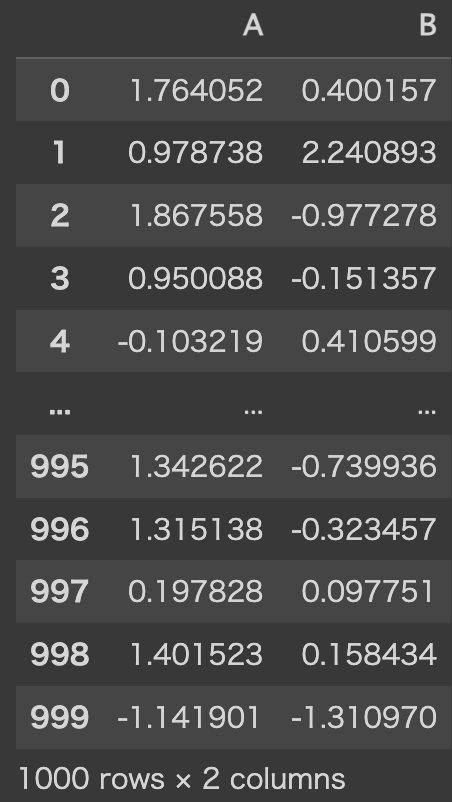
次に、A列とB列の値から以下の通りC列、D列、E列を計算します。
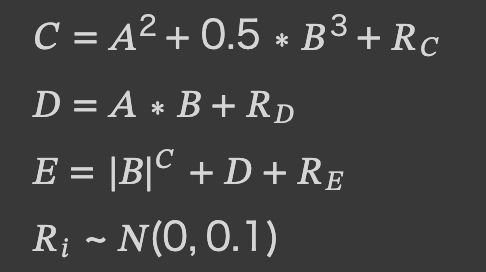
ここで、Riは平均0、標準偏差0.1に従う正規乱数。
X['C'] = X.apply(lambda x: x['A'] + 0.5 * (x['B'] ** 3) + np.random.normal(scale=0.1), axis='columns')
X['D'] = X.apply(lambda x: x['A'] * x['B'] + np.random.normal(scale=0.1), axis='columns')
X['E'] = X.apply(lambda x: (abs(x['B']) ** x['C']) + x['D'] + np.random.normal(scale=0.1), axis='columns')
X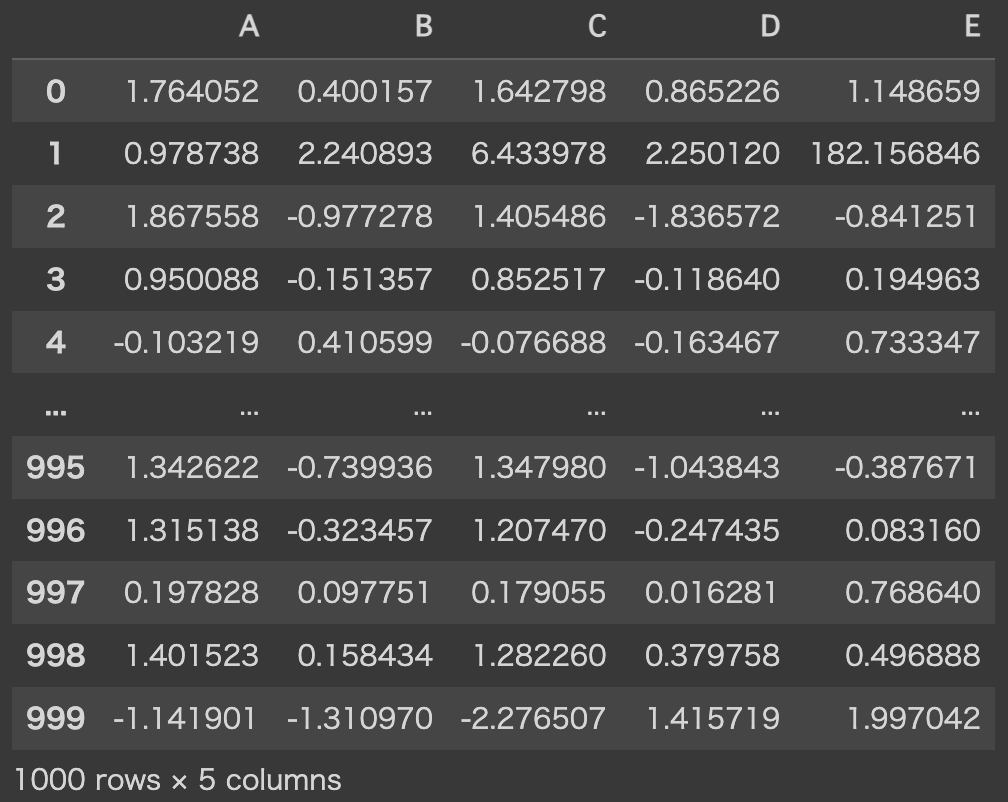
そして、各列に対してランダムに20%のデータを欠損させます。
X_missed = X.copy()
for column in X_missed.columns:
X_missed.loc[np.random.choice(X_missed.index, size=(int(len(X_missed) * 0.2)), replace=False), column] = np.nan
X_missed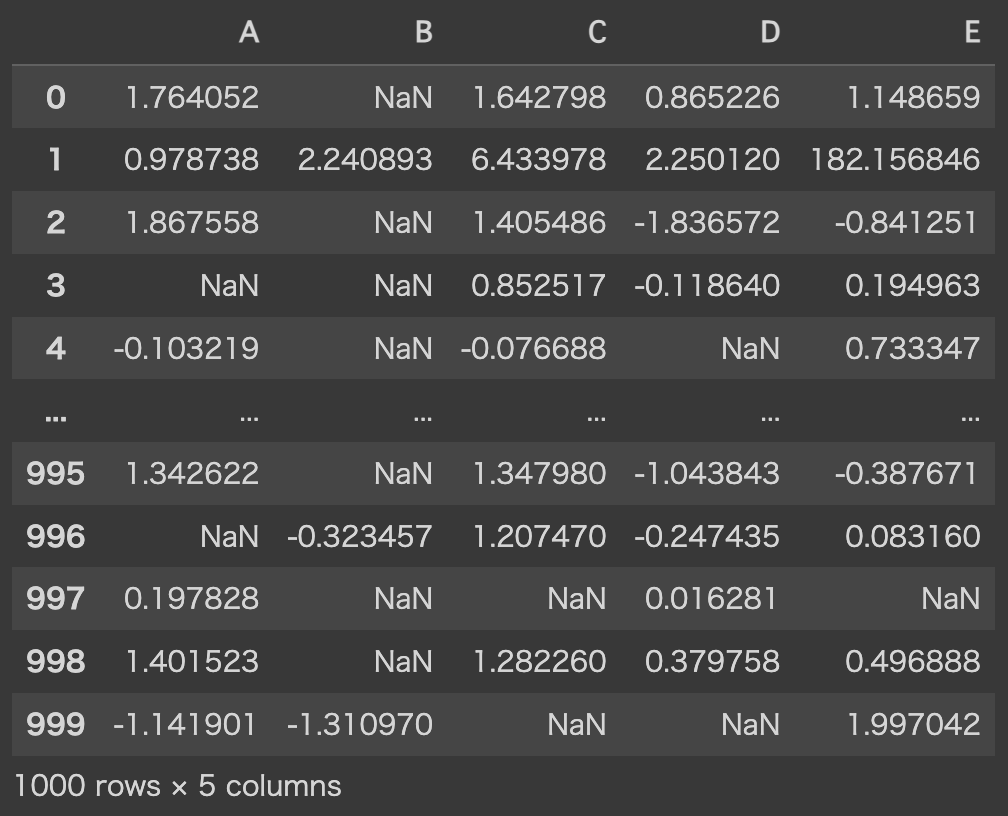
最後に、以上の手順によって 生成した仮想的な生データ𝑋𝑚𝑖𝑠𝑠𝑒𝑑の各列の分布と変数間の関係を視覚的に確認しておきます。
mport matplotlib.pyplot as plt
import seaborn as sns; sns.set()
sns.pairplot(X_missed)
A列からD列については、それぞれの変数間に非線形な関係があることが視覚的に確認できます。
E列は、少しトリッキーな初項|𝐵|𝐶によって分布や他変数との関係が極端になっています。
利用方法
まずはモジュールをインポートします。
一応、IterativeImputerは2024年6月14日現在においてexperimental(実験的)扱いなモジュールのため、今後のバージョンアップや仕様変更にはご注意ください。
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer次に、補完器を定義し、対象のデータを学習させます。
imputer = IterativeImputer(random_state=0)
imputer.fit(X_missed)そして、欠損データを補完器に通し、補完後データを出力します。
補完器に通すデータは学習データと同一物である必要はなく、違っていても(=アウトサンプルでも)構いませんが、今回は学習に用いたデータを全部そのまま補完器に通します。
X_imputed = pd.DataFrame(imputer.transform(X_missed), columns=X_missed.columns)
X_imputed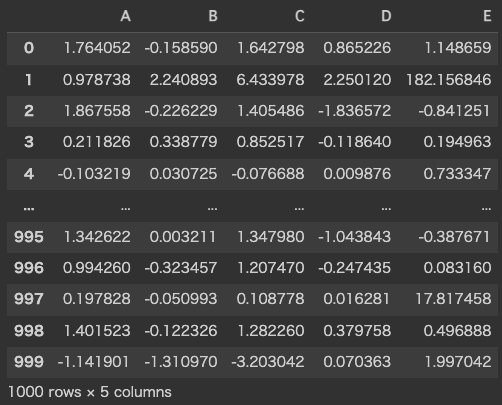
最後に、補完後データ𝑋𝑖𝑚𝑝𝑢𝑡𝑒𝑑の分布と変数間の関係も確認してみましょう。
sns.pairplot(X_imputed)
見た目は欠損させる前の正解データ𝑋とさほど変わりません。
パフォーマンス評価
まず比較対象として、平均値・中央値・最頻値の3種類の単変量補完データを計算します。
X_mean = X_missed.fillna(X_missed.mean())
X_median = X_missed.fillna(X_missed.median())
X_mode = X_missed.fillna(X_missed.mode())そして、前節で計算したIterativeImputerによる多変量補完データ𝑋𝑖𝑚𝑝𝑢𝑡𝑒𝑑を含めた4種類の補間後データに対し、正解データ𝑋との各列の相関を計算し、棒グラフにプロットします。
performance = pd.concat([
X.apply(lambda x: x.corr(X_imputed[x.name])).rename('IterativeImputer'),
X.apply(lambda x: x.corr(X_mean[x.name])).rename('mean'),
X.apply(lambda x: x.corr(X_median[x.name])).rename('median'),
X.apply(lambda x: x.corr(X_mode[x.name])).rename('mode'),
], axis='columns').T
display(performance)
performance.T.plot(kind='bar')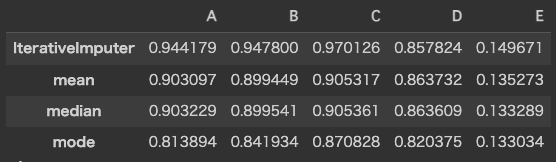
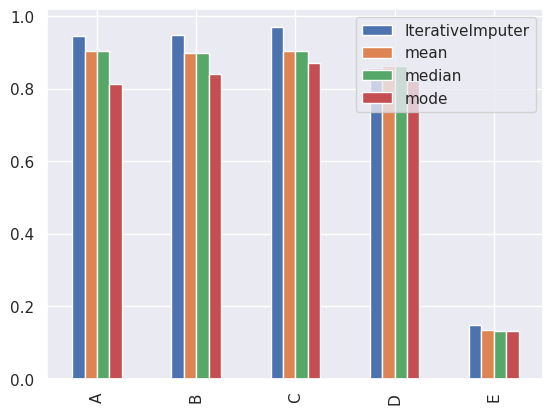
まず、IterativeImputerを含むどの手法もE列のパフォーマンスは総じて良くなかったことが確認できます。やはり、トリッキーな数式を用いて算出したE列の再現は難しかったようです。
ただ、E列はそもそもの分布に外れ値があるので、外れ値に強いスピアマンの順位相関を使って同じことをしてみます。
performance_spearman = pd.concat([
X.apply(lambda x: x.corr(X_imputed[x.name], method='spearman')).rename('IterativeImputer'),
X.apply(lambda x: x.corr(X_mean[x.name], method='spearman')).rename('mean'),
X.apply(lambda x: x.corr(X_median[x.name], method='spearman')).rename('median'),
X.apply(lambda x: x.corr(X_mode[x.name], method='spearman')).rename('mode'),
], axis='columns').T
display(performance_spearman)
performance_spearman.T.plot(kind='bar')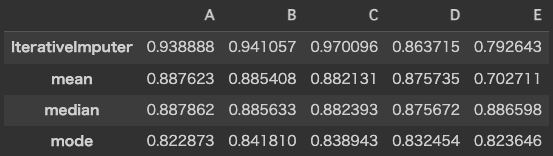
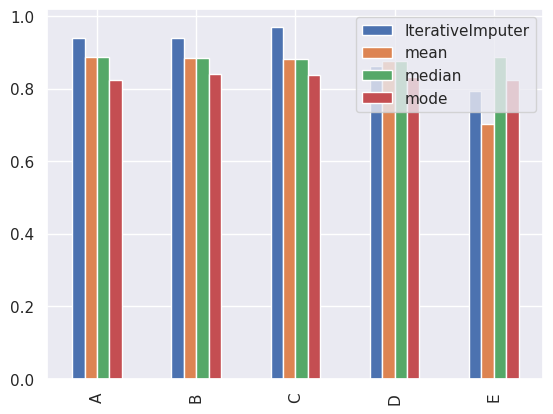
スピアマンの順位相関では、E列の相関も他の列と遜色ない水準になり、E列自身の分布の特殊性の影響をある程度緩和できそうです。
次に、各手法の相対感をみるため、A列~E列の各列に対して(スピアマンの)相関係数の平均値を差し引き、棒グラフにプロットします。
performance_relative = performance_spearman.apply(lambda x: x - x.mean())
performance_relative['total'] = performance_relative.mean(axis='columns')
display(performance_relative)
performance_relative.T.plot(kind='bar')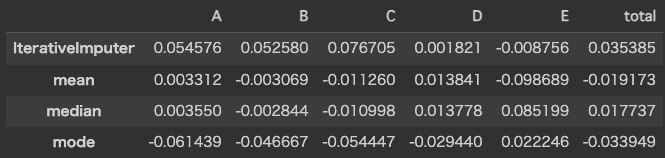
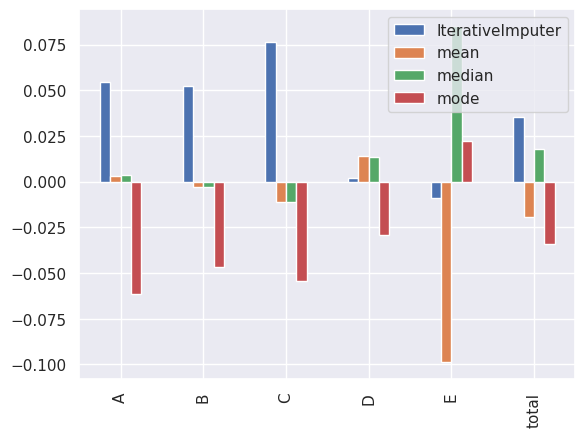
D列やE列については、IterativeImputerは単変量補完に若干劣る結果となりましたが、総合的にみてIterativeImputerのパフォーマンスが最も良かったことを確認できました。
まとめ
- 単変量補完と多変量補完の理論的概要、メリット・デメリットを解説しました。
- 特に、実務における多くの場面では多変量補完でよく、多変量補完の汎用性の高さを指摘しました。
- Pythonのscikit-learnライブラリにおけるIterativeImputerの利用方法を解説しました。
- 乱数により生成した仮想的データを用いて、IterativeImputerのパフォーマンスを数値的に実験し、単変量補完に比べて概ね優位な結果が得られたことを確認しました。